Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1
Question 1.
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
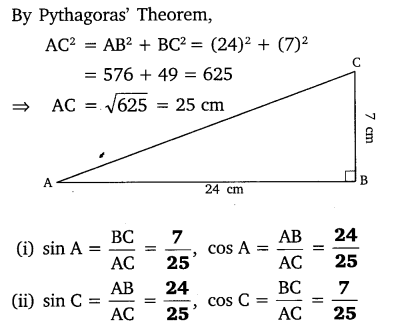
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:

Question 2.
In given figure, find tan P – cot R.
Solution:

In given figure, find tan P – cot R.
Solution:

Question 3.
If sin A = , calculate cos A and tan A.
, calculate cos A and tan A.
Solution:
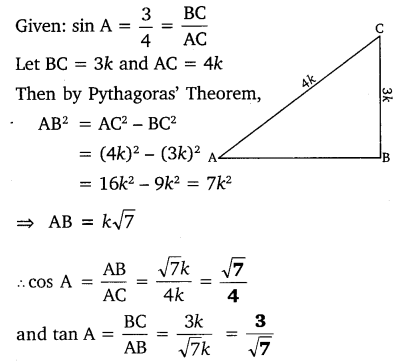
If sin A =
Solution:
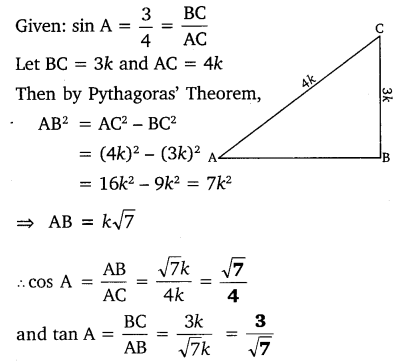
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:

Given 15 cot A = 8, find sin A and sec A.
Solution:

Question 5.
Given sec θ =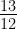 , calculate all other trigonometric ratios.
, calculate all other trigonometric ratios.
Solution:

Given sec θ =
Solution:

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:

Question 7.
If cot θ =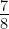 , evaluate:
, evaluate:
(i)
(ii) cot²θ
Solution:

If cot θ =
(i)
(ii) cot²θ
Solution:

Question 8.
If 3 cot A = 4, check whether = cos² A – sin² A or not.
= cos² A – sin² A or not.
Solution:

If 3 cot A = 4, check whether
Solution:

Question 9.
In triangle ABC, right angled at B, if tan A =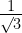 , find the value of:
, find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:

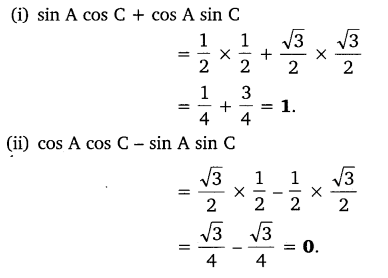
In triangle ABC, right angled at B, if tan A =
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:

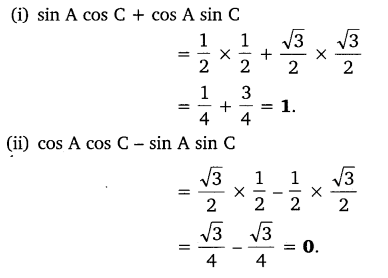
Question 10.
In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:

Question 11.
State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = for some value of angle A.
for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = for some angle.
for some angle.
Solution:

State whether the following statements are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A =
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ =
Solution:

Chapter 8 Introduction to Trigonometry Ex 8.2
Question 1.
Evaluate the following:

Solution:
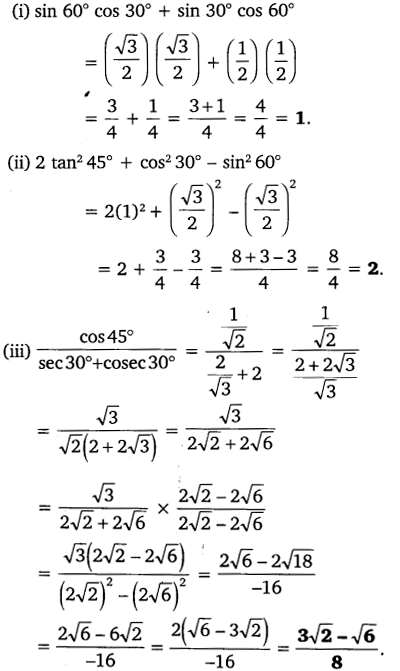
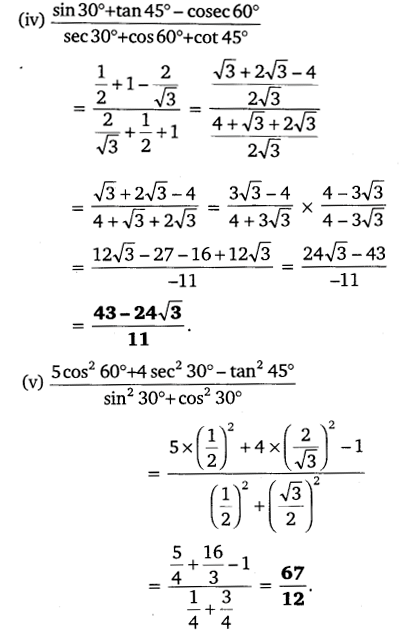
Evaluate the following:

Solution:
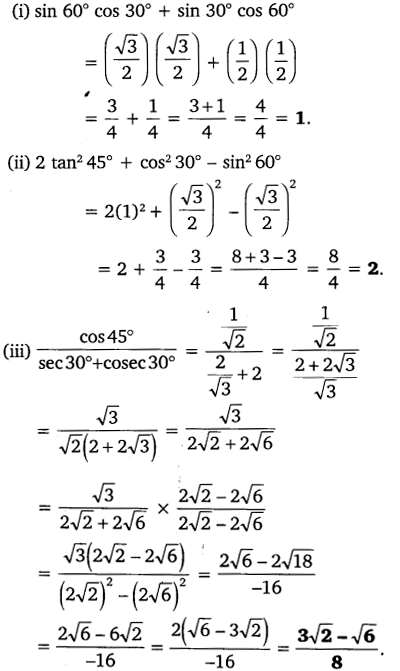
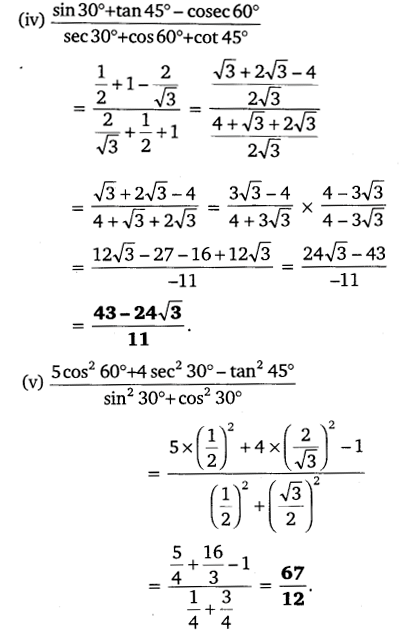
Question 2.
Choose the correct option and justify your choice:

Solution:

Choose the correct option and justify your choice:

Solution:

Question 3.
If tan (A + B) = √3 and tan (A – B) =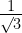 ; 0° < A + B ≤ 90°; A > B, find A and B.
; 0° < A + B ≤ 90°; A > B, find A and B.
Solution:
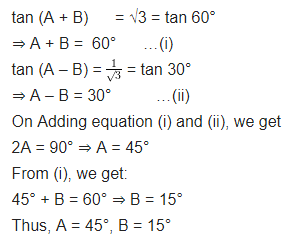
If tan (A + B) = √3 and tan (A – B) =
Solution:
Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution:
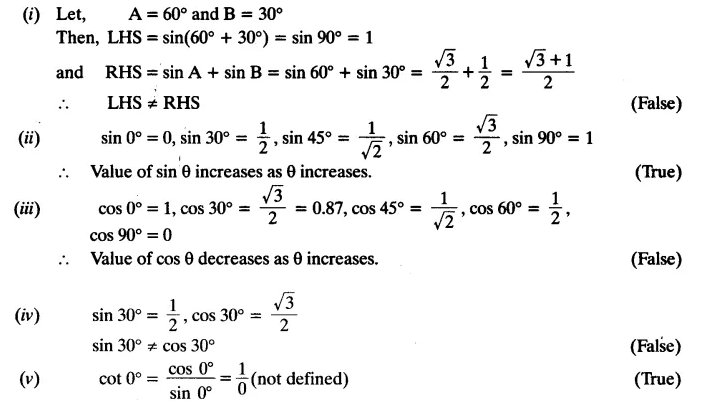
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution:
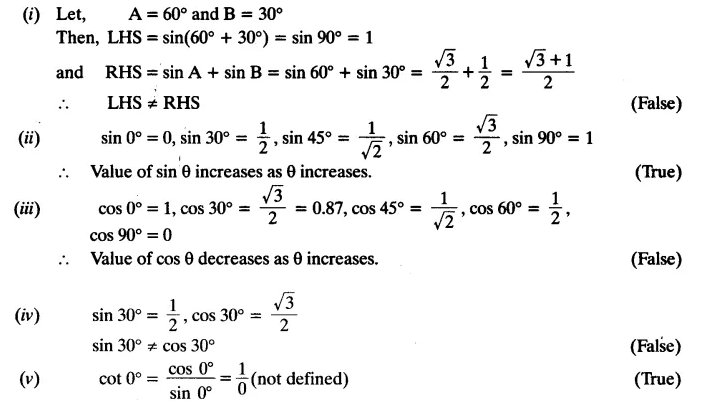
Introduction to Trigonometry Ex 8.3
Question 1.
Evaluate:

Solution:
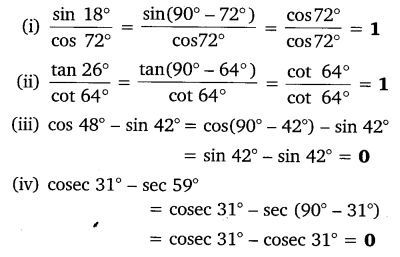
Evaluate:
Solution:
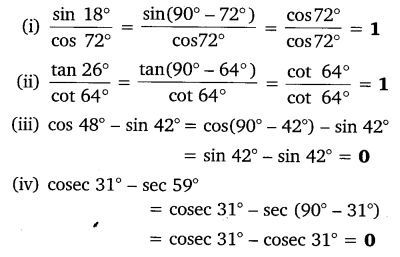
Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:

Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:

Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
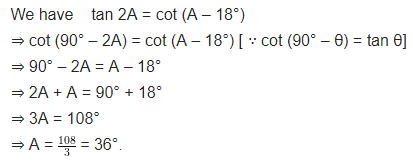
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
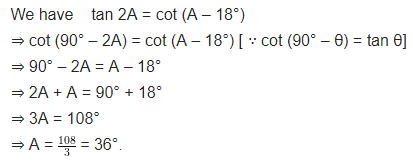
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
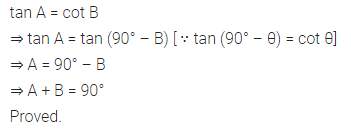
If tan A = cot B, prove that A + B = 90°.
Solution:
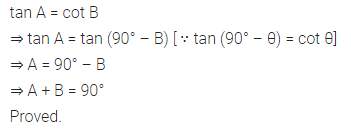
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
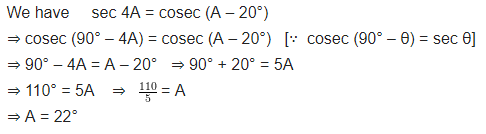
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
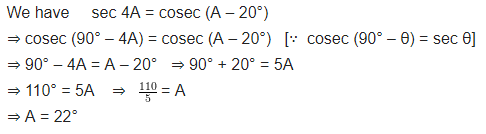
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that: sin ( ) = cos
) = cos 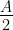
Solution:
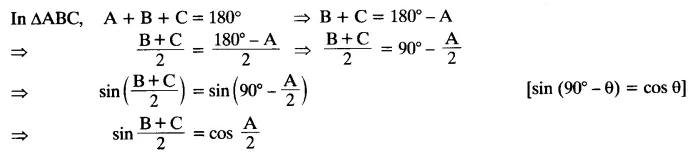
If A, B and C are interior angles of a triangle ABC, then show that: sin (
Solution:
Question 7.
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
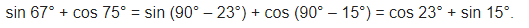
Express sin 61° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
Trigonometry Ex 8.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:

Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
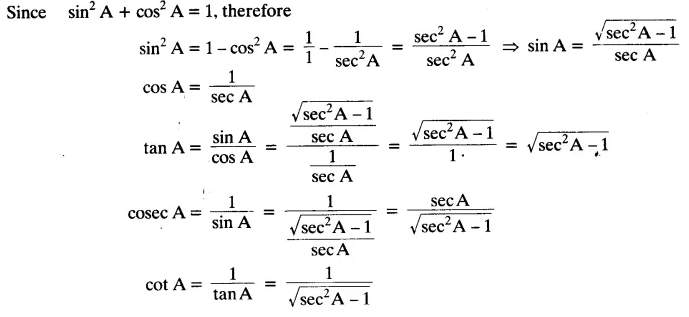
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:

Question 3.
Evaluate:

Solution:
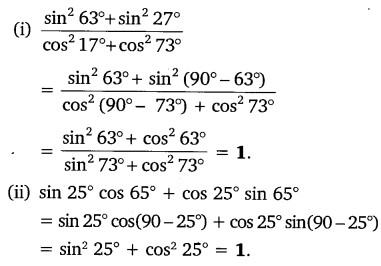
Evaluate:

Solution:
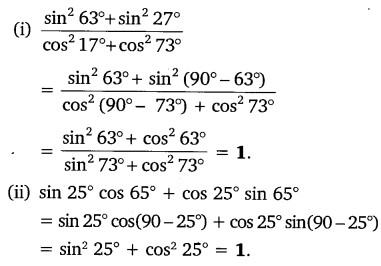
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1
(B) 9
(C) 8
(D) 0
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A = ……
(A) 1
(B) 9
(C) 8
(D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) = ………..
(A) 0
(B) 1
(C) 2
(D) -1
(A) 0
(B) 1
(C) 2
(D) -1
(iii) (sec A + tan A) (1 – sin A) = ………….
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
(iv) 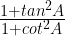 = ………..
= ………..
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
Solution:

(A) sec² A
(B) -1
(C) cot² A
(D) tan² A
Solution:

Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Solution:

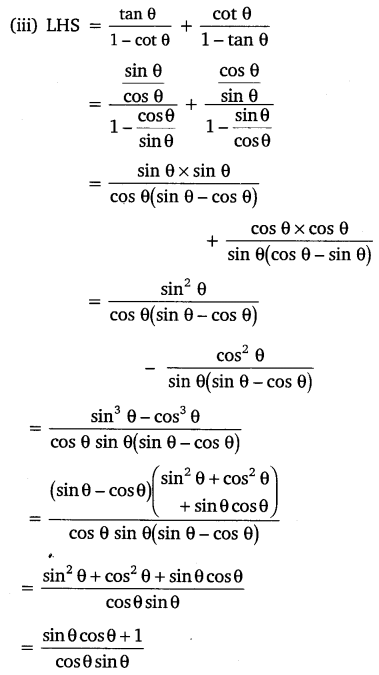

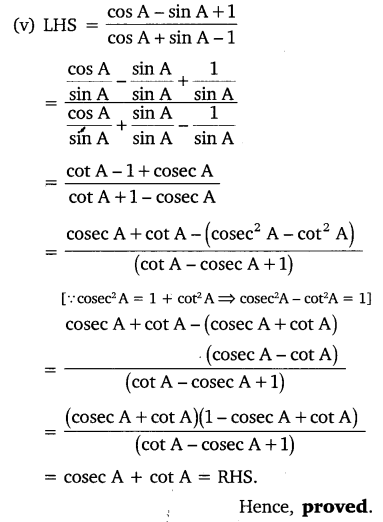


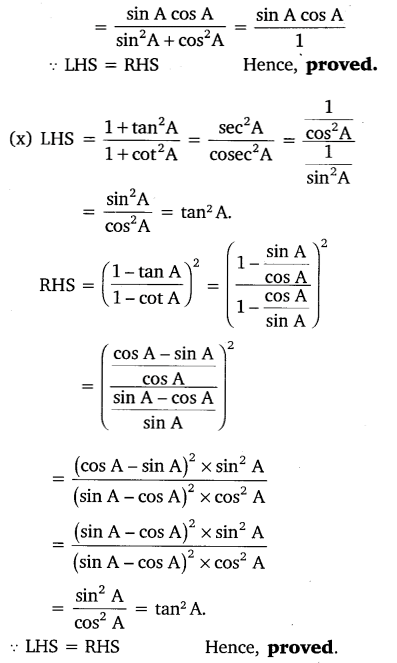
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

Solution:

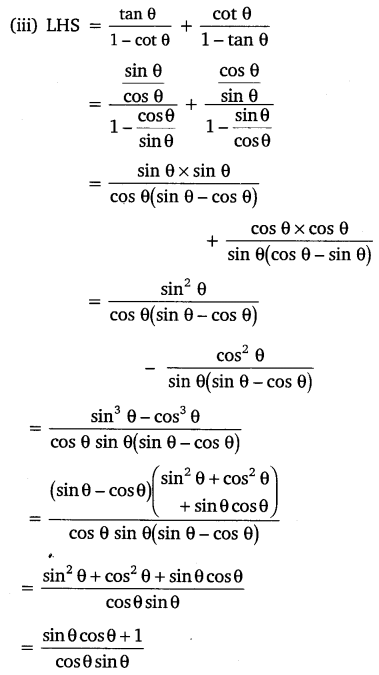

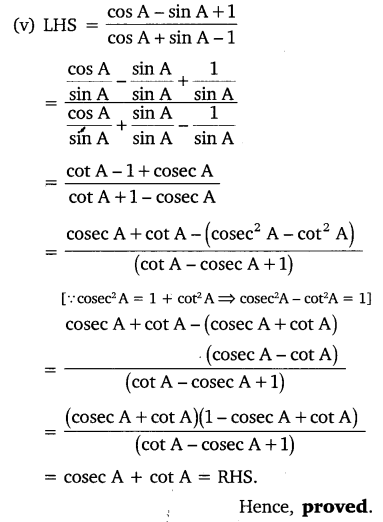



Comments
Post a Comment