Pair of Linear Equations in Two Variables Ex 3.1
Question 1.Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. Isn’t this interesting? Represent this situation algebraically and graphically.
Solution:
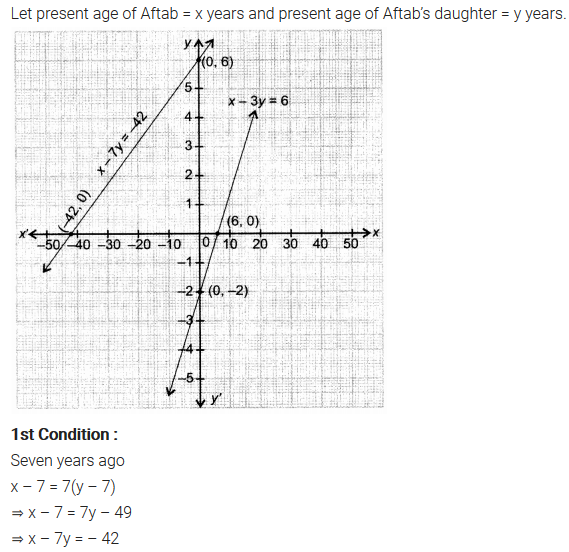

Solution:


Question 2.The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300. Represent this situation algebraically and geometrically.
Solution:
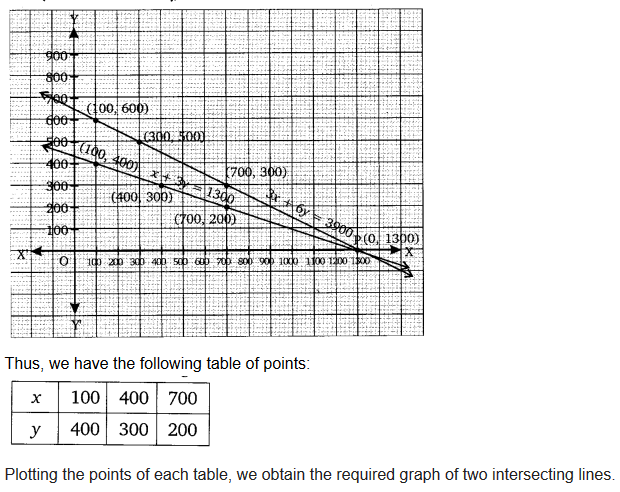
Solution:


Question 3.The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹300. Represent the situation algebraically and geometrically.
Solution:
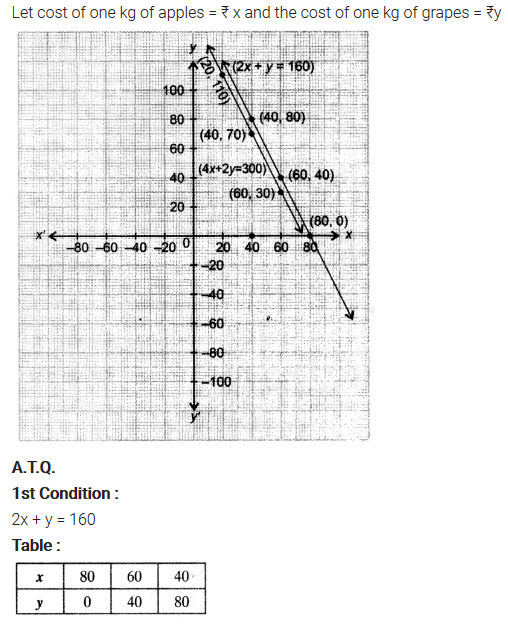

Solution:


Pair of Linear Equations in Two Variables Ex 3.2
Question 1. Form the pair of linear equations of the following problems and find their solutions graphically:
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
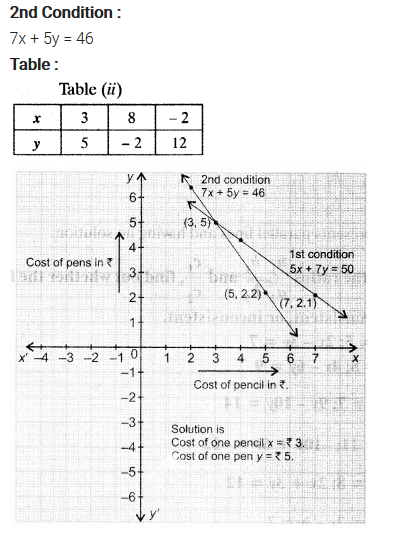
(ii) 5 pencils and 7 pens together cost ₹50, whereas 7 pencils and 5 pens together cost ₹46. Find the cost of one pencil and that of one pen.
Solution:

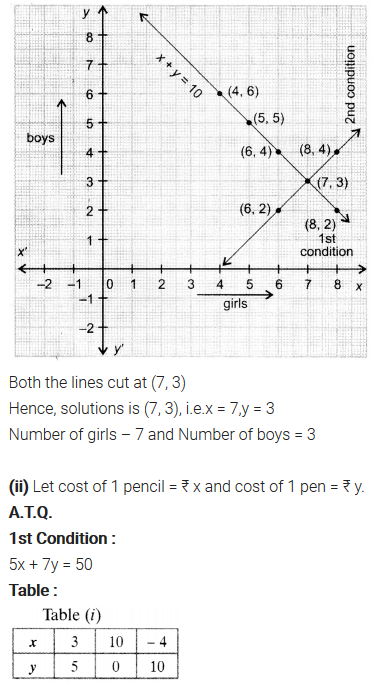
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹50, whereas 7 pencils and 5 pens together cost ₹46. Find the cost of one pencil and that of one pen.
Solution:



Question 2.
On comparing the ratios 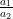 ,
, 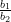
and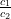 , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 0, 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0, 2x -y + 9 = 0
Solution:


and
(i) 5x – 4y + 8 = 0, 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0, 2x -y + 9 = 0
Solution:


Question 3.On comparing the ratios 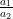 ,
, 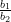
and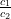 , find out whether the following pairs of linear equations are consistent, or inconsistent:
, find out whether the following pairs of linear equations are consistent, or inconsistent:
~
Solution:

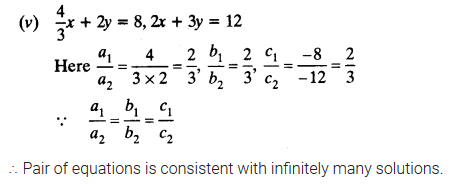
and
~
Solution:

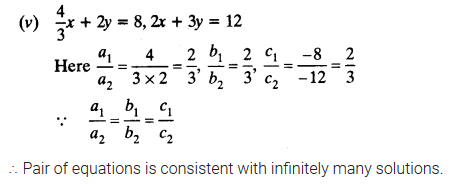
Question 4.Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically.
(i) x + y = 5, 2x + 2y = 10
(ii) x-y – 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solution:
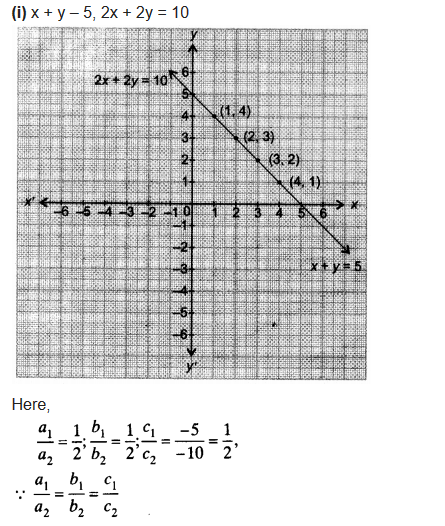

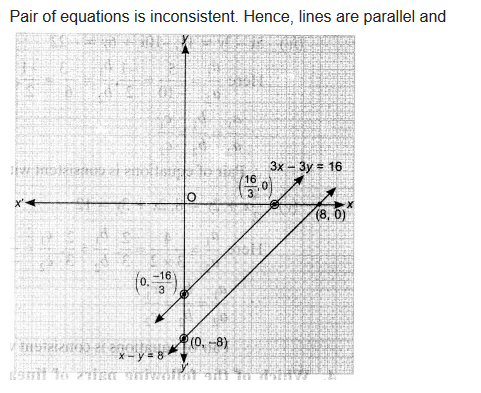

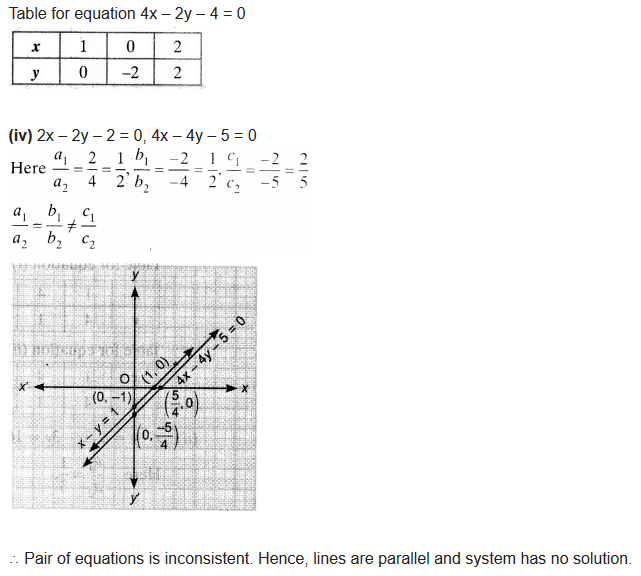
(i) x + y = 5, 2x + 2y = 10
(ii) x-y – 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solution:





Question 5.Half the perimeter of a rectangular garden, whose length is 4 m more than its width is 36 m. Find the dimensions of the garden graphically.
Solution:

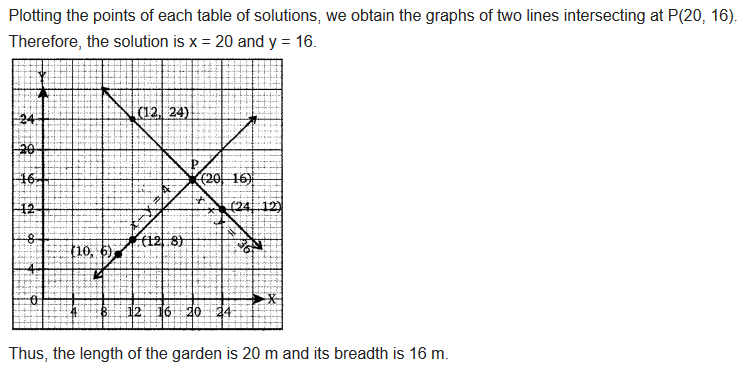
Solution:


Question 6.Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
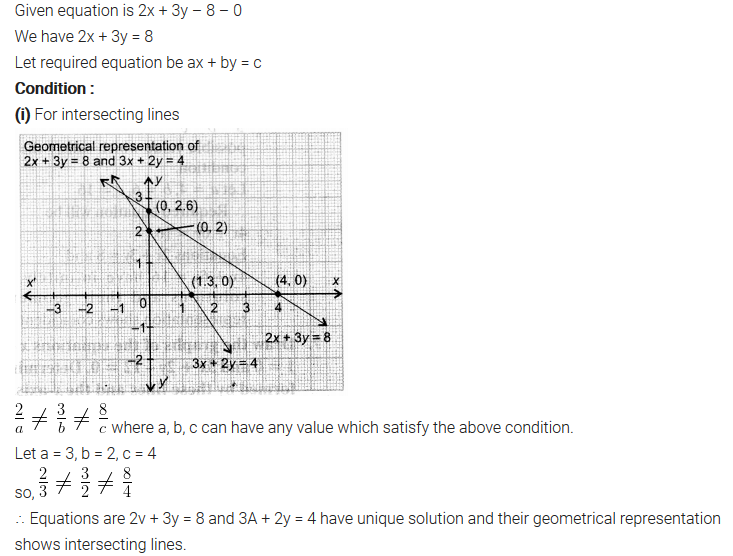
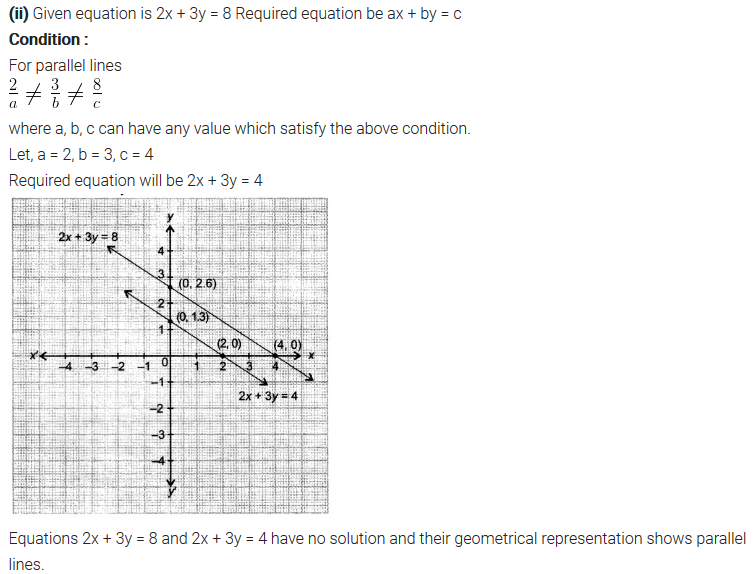
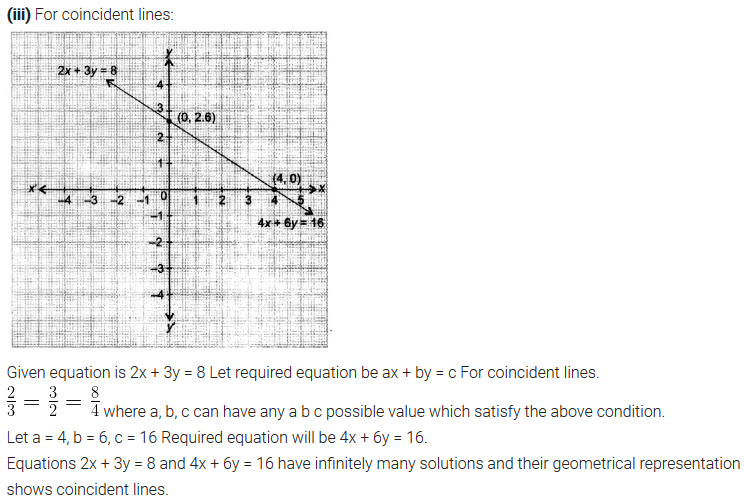
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:



Question 7.
Draw the, graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:
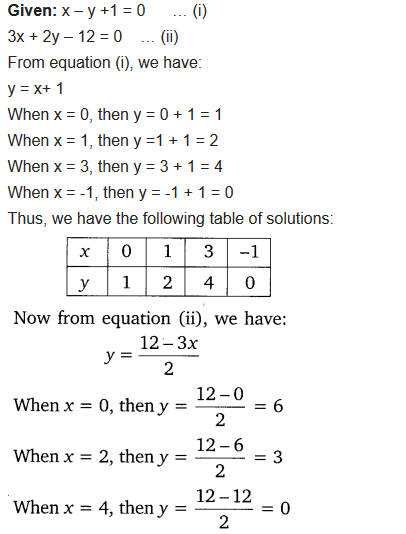
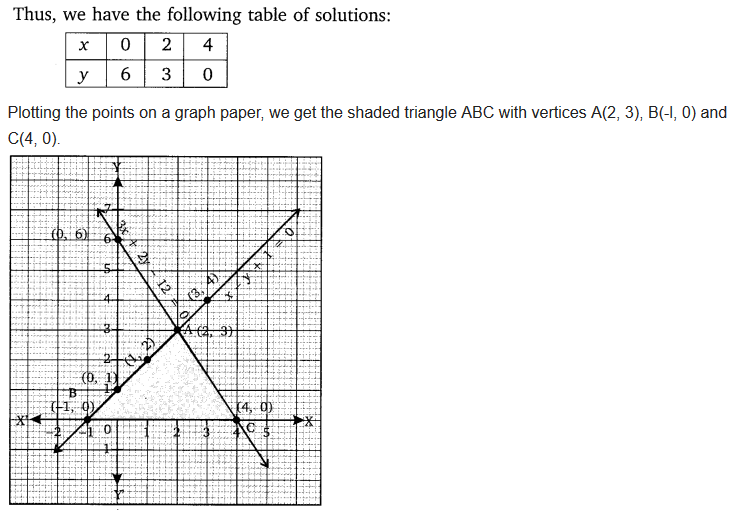
Solution:
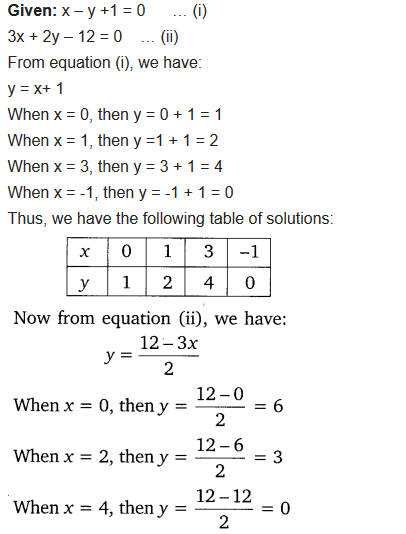

Pair of Linear Equations in Two Variables Ex 3.3
Question 1.Solve the following pairs of linear equations by the substitution method:

Solution:
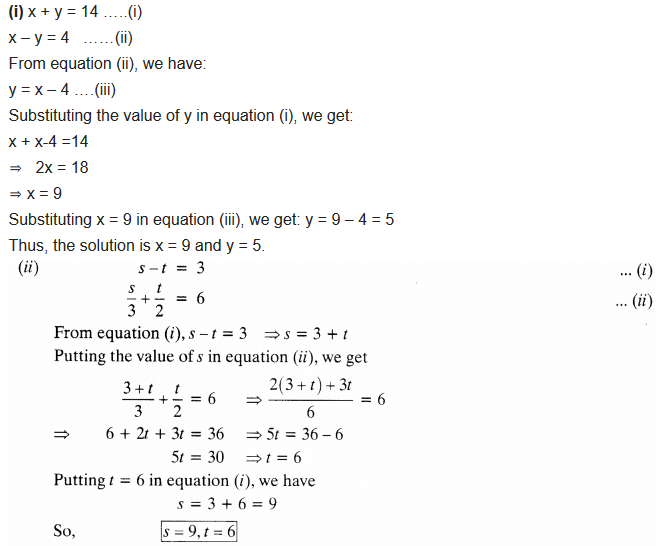

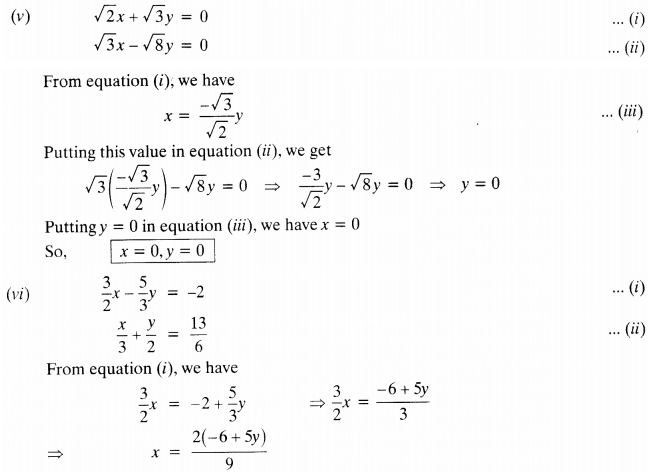
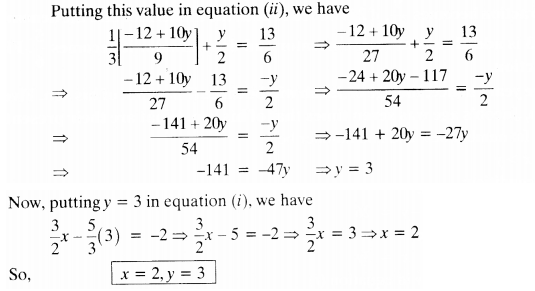

Solution:
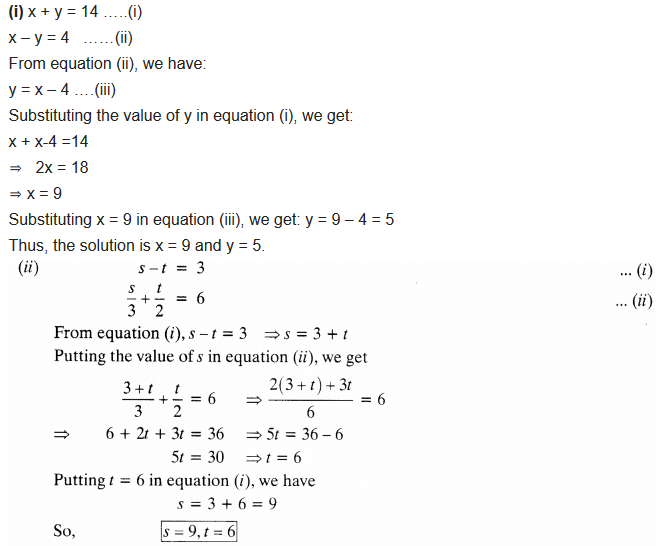

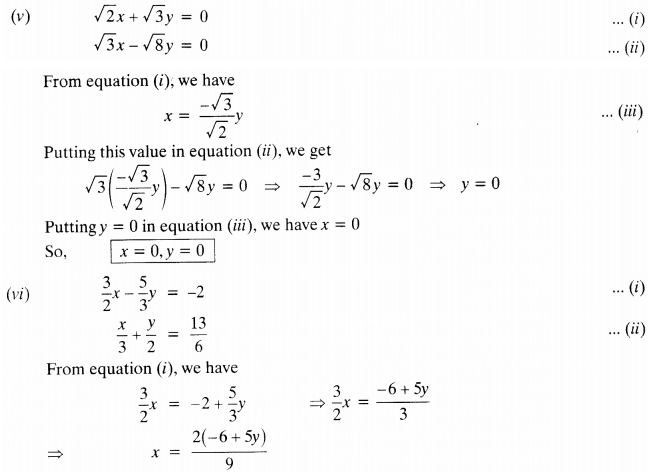
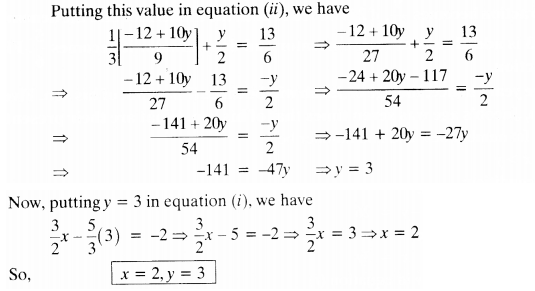
Question 2.
Solve 2x + 3y = 11 and 2x – 4y = -24 and hence find the value of’m’ for which y = mx +3.
Solution:

Solution:

Question 3.Form the pair of linear equations for the following problems and find their solution by substitution method:
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
(iii) The coach of a cricket team buys 7 bats and 6 balls for ₹3800. Later, she buys 3 bats and 5 balls for ₹1750. Find the cost of each bat and each ball.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ₹105 and for a journey of 15 km, the charge paid is ₹155. What are the fixed charges and the charges per km? How much does a person have to pay for travelling a distance of 25 km?
(v) A fraction becomes , if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes
, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes 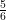 . Find the fraction.
. Find the fraction.
(vi) Five years hence, the age of Jacob will be three times that of his son. Five year ago, Jacob’s age was seven times that of his son. What are their present ages?
Solution:




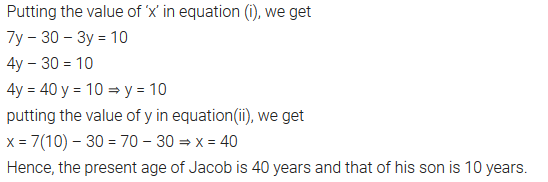
(i) The difference between two numbers is 26 and one number is three times the other. Find them.
(ii) The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
(iii) The coach of a cricket team buys 7 bats and 6 balls for ₹3800. Later, she buys 3 bats and 5 balls for ₹1750. Find the cost of each bat and each ball.
(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ₹105 and for a journey of 15 km, the charge paid is ₹155. What are the fixed charges and the charges per km? How much does a person have to pay for travelling a distance of 25 km?
(v) A fraction becomes
(vi) Five years hence, the age of Jacob will be three times that of his son. Five year ago, Jacob’s age was seven times that of his son. What are their present ages?
Solution:









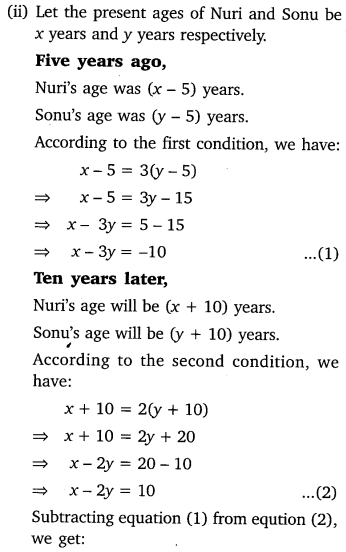





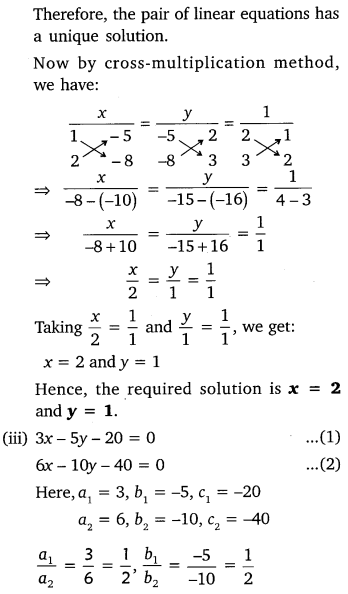
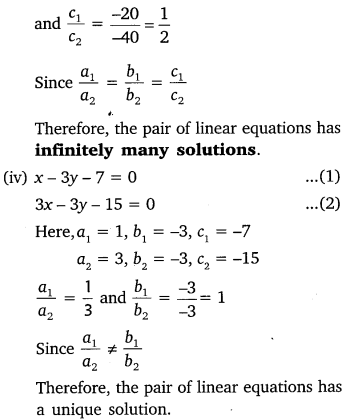


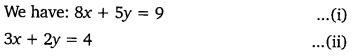

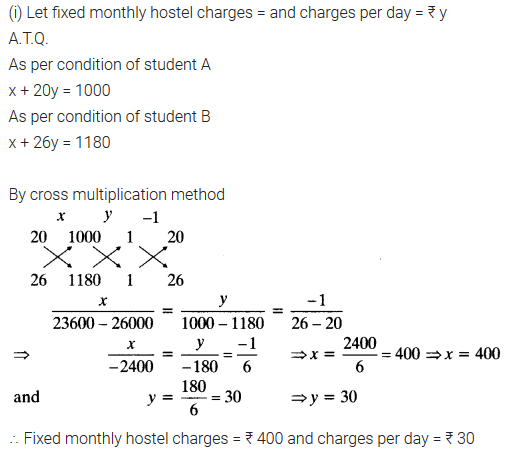

Comments
Post a Comment