Question 1.
How many tangents can a circle have?
Solution:
There can be infinitely many tangents to a circle.
Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a ………… .
(iii) A circle can have ………………. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ……….. .
Solution:

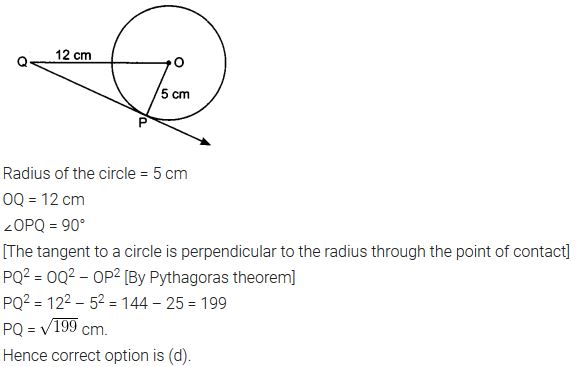
Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) cm
cm
Solution:
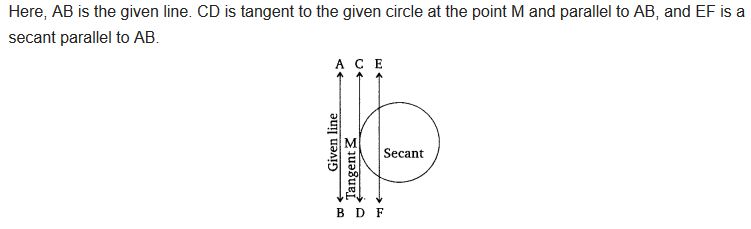
Question 4.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
How many tangents can a circle have?
Solution:
There can be infinitely many tangents to a circle.
Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a ………… .
(iii) A circle can have ………………. parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called ……….. .
Solution:

Question 3.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d)
Solution:

Question 4.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:

Chapter 10 Circles Ex 10.2
Chapter 10 Circles Ex 10.2
In Q.1 to 3 choose the correct option and give justification.
Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
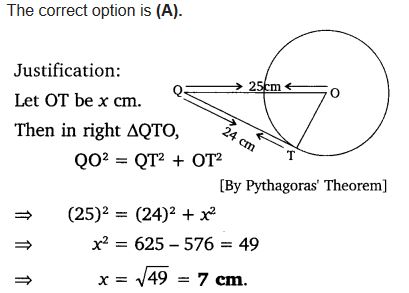
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:

Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°

Solution:
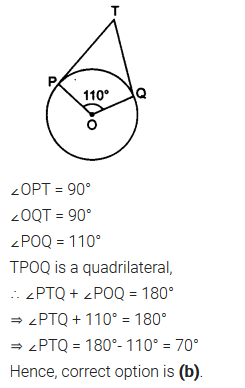
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°

Solution:

Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
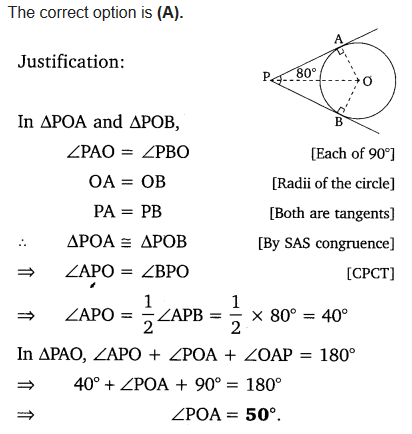
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
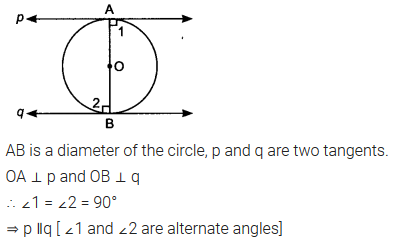
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:

Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
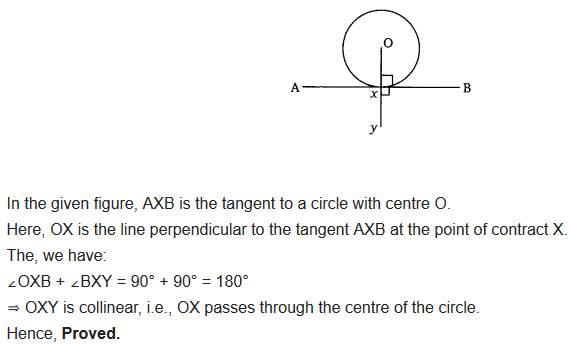
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:

Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
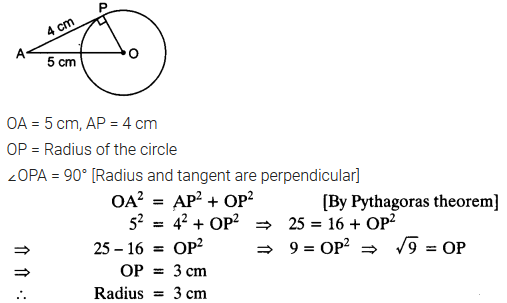
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
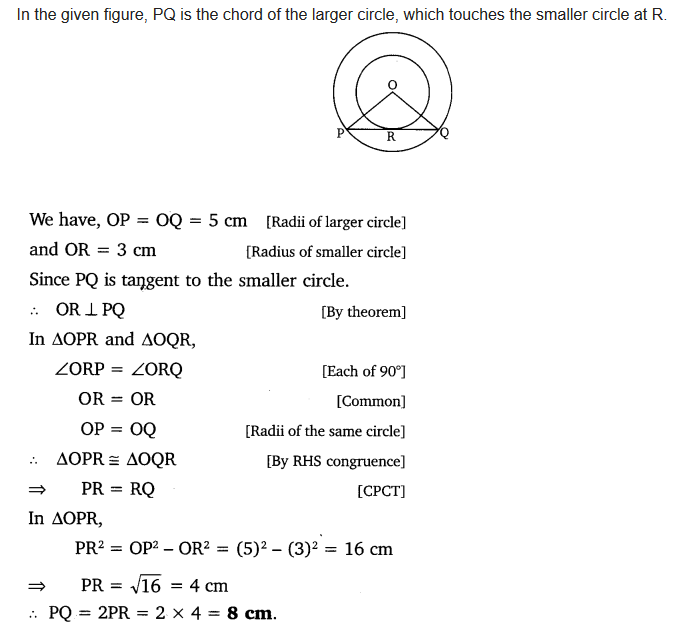
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
 Solution:
Solution:
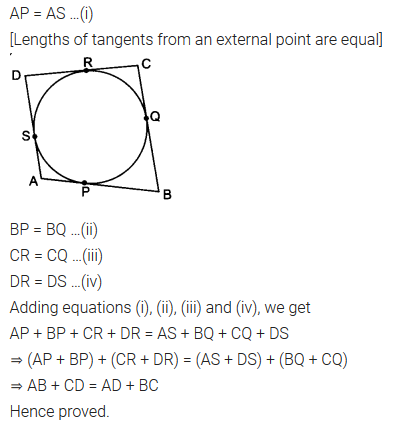
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
 Solution:
Solution:
Question 9.
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
 Solution:
Solution:

In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
 Solution:
Solution:
Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
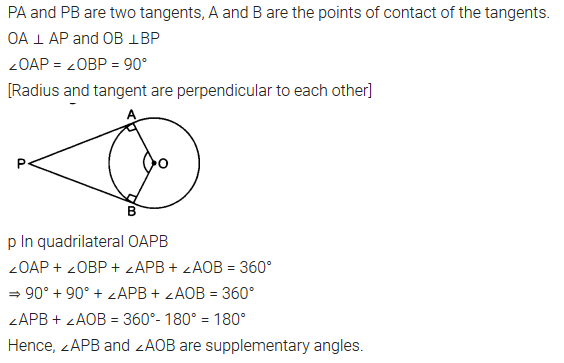
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:

Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
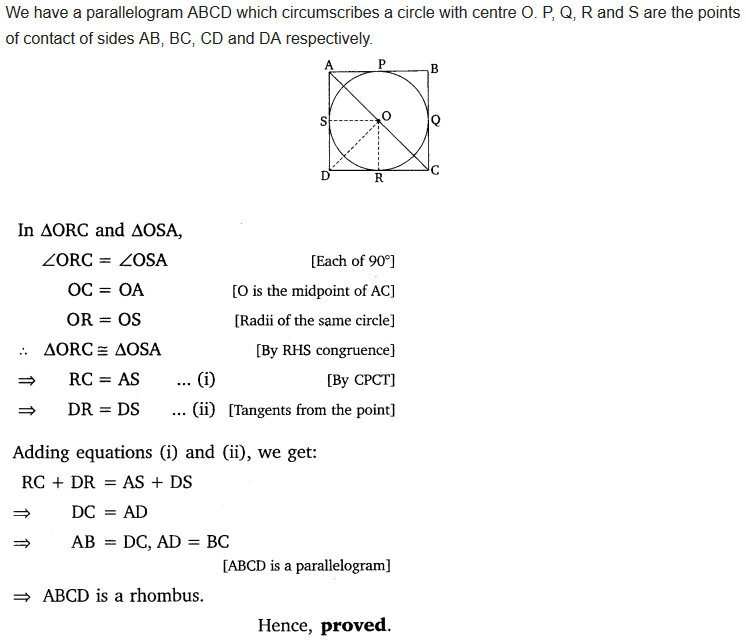
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:

Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
 Solution:
Solution:
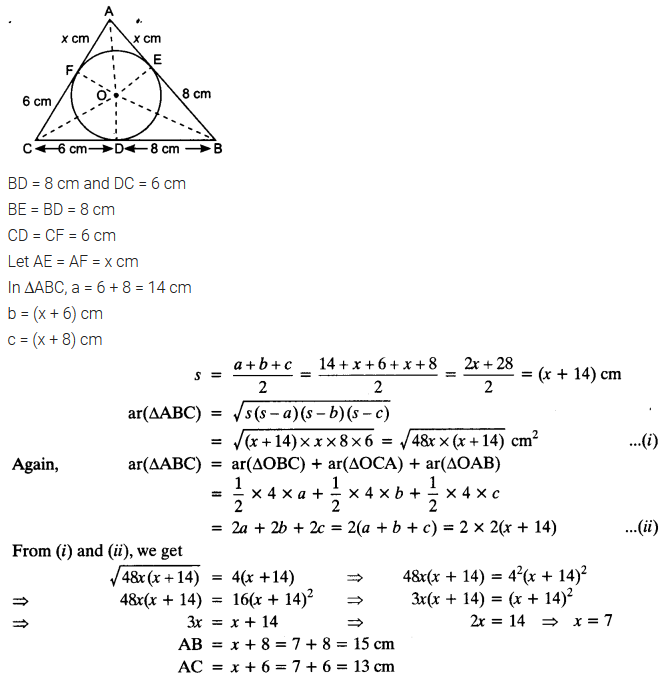
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
 Solution:
Solution:
Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
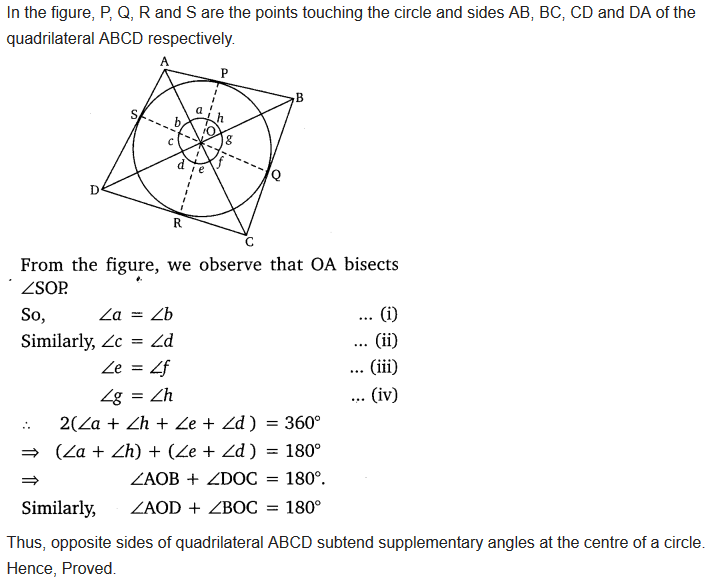
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:

Comments
Post a Comment