Question 1.
Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
 Solution:
Solution:

Find the area of the shaded region in the given figure, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
 Solution:
Solution:
Question 2.
Find the area of the shaded region in the given figure, ¡f radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
 Solution:
Solution:

Find the area of the shaded region in the given figure, ¡f radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.
 Solution:
Solution:
Question 3.
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
 Solution:
Solution:

Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
 Solution:
Solution:
Question 4.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
 Solution:
Solution:

Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
 Solution:
Solution:
Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.
 Solution:
Solution:

From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.
 Solution:
Solution:
Question 6.
In a circular table cover of (he radius 32 cm, a design Is formed leaving an equilìtcral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region). Solution:
Solution:
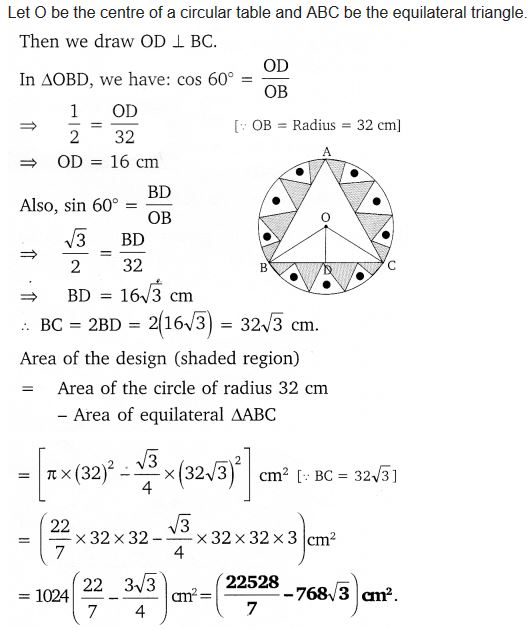
In a circular table cover of (he radius 32 cm, a design Is formed leaving an equilìtcral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region).
 Solution:
Solution:
Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:

In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Solution:

Question 8.
The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
 (i) the distance around the track along its inner edge.
(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:
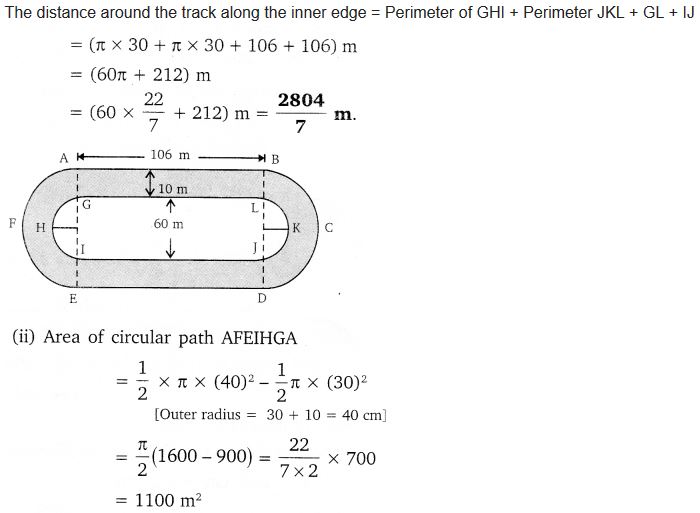

The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
 (i) the distance around the track along its inner edge.
(i) the distance around the track along its inner edge.(ii) the area of the track.
Solution:


Question 9.
In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
 Solution:
Solution:

In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
 Solution:
Solution:
Question 10.
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region.
(Use π = 3.14 and √ 3 = 1.73205).
 Solution:
Solution:

The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region.
(Use π = 3.14 and √ 3 = 1.73205).
 Solution:
Solution:
Question 11.
On a square handkerchief, nine circular designs each of the radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
 Solution:
Solution:

On a square handkerchief, nine circular designs each of the radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
 Solution:
Solution:
Question 12.
In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
 Solution:
Solution:

In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
 Solution:
Solution:
Question 13.
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
 Solution:
Solution:

In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)
 Solution:
Solution:
Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ZAOB=30°, find the area of the shaded region.
 Solution:
Solution:

AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ZAOB=30°, find the area of the shaded region.
 Solution:
Solution:
Question 15.
In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
 Solution:
Solution:

In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
 Solution:
Solution:
Question 16.
Calculate the area of the designed region in the figure common between the two quadrants of the circles of the radius 8 cm each.
 Solution:
Solution:
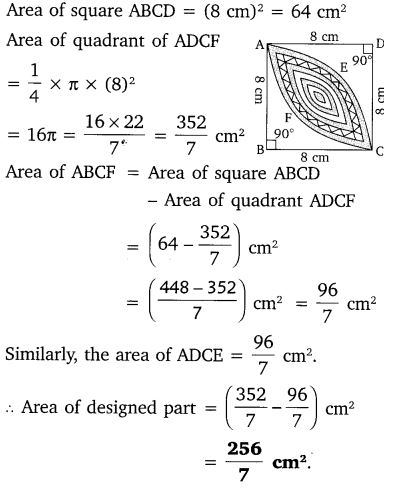
Calculate the area of the designed region in the figure common between the two quadrants of the circles of the radius 8 cm each.
 Solution:
Solution:
Comments
Post a Comment